Isomorphisms Between Time and Tone

Introduction

The musical domains of tone and time are commonly distinguished when discussing sound art. Different cultures and their musical traditions can be discerned by the various perspectives and systems they employ when engaging with these domains. There is evidence to support that various musics from around the world exhibit structural similarities across their manipulations of tone and time. These similarities can be mapped in the form of isomorphic or identical models. While perceptually, these domains appear strikingly different, the existence of such isomorphisms hints at the possibility that they share fundamental commonalities in the ways they are processed cognitively.

Several articles explore these structural similarities from different perspectives (Pressings 1983, London 2002, Rahn 1975, Stevens 2004, Bar-Yosef 2007, etc.), alluding to a myriad of possibilities for connection. In the West, electronic music brought about considerations of time and tone— most notably, Stockhausen (in *Structure and Experimential Time* and *The Concept of Unity in Electronic Music*) and Grisey (in *Tempus Ex Machina*). The book, *Microsound*, by composer Curtis Roads tackles this subject and provides helpful references to other composers in this vein.

The goal of this paper is to identify and discuss models which can effectively relate various musical phenomena across the domains of time and tone. I will explore the theoretical understanding for such isomorphisms, both reviewing established and introducing new models. Beginning with a brief review on select physical properties of sound, I will explore the perceptual distinction which separates these two domains. This understanding will inform the investigation and evaluation of subsequent theoretical equivalences. I will compare the pertinence of models by comparing their ability relate unique or multiple musical phenomena. Evaluation will be judged through the perspectives oriented around perception/cognition, relevance to existing music (general musicology), and through the functional limitations of the models.

The Fundamental Problem

When considering the perceptually disparate concepts of time and tone, it is helpful to begin at the instance in which both are physically identical: pulsation and frequency. A frequency is the rate at which air pressure cycles in and out of equilibrium. A pulsation is an onset which recurs at a single constant duration. For purposes of clarity, I will briefly ignore the specific onset/offset amplitude envelopes and refer to each unit of pressure disturbance as a grain- a sufficiently brief sonic impulse. We can merge these definitions by claiming that both frequency and pulsation are periods of pressure disturbance (or grains); regarding pulsation as a slow frequency (<20Hz) and pitch as a fast pulsation (>20Hz). For clarity, I associate pulsation with rhythm/time and frequency with pitch/tone in this paper.

In order to begin, it is first necessary to understand how a single physical stream of events manifests into the two disparate perceptions of tone and time. We can do this through a simple example. Take a chain of identical grains pulsating steadily at a rate of five times per second (5Hz). This chain will be heard as five discrete points within each passing second. However, as the grains repeat faster (the inter-onset interval (IOI) decreases) than 20 grains per second (20Hz), the perception of an individual grain is no longer possible. Where each individual grain was once identifiable, instead the IOI- the amount of time between each grain- is “listened to” and abstracted into a *tone*. The sensation of pitch occurs when grains are replaced by the perception of a temporally-abstract (“atemporal”) tone. In other words, discrete grains pulsating at 500Hz are not perceived as 500 events, but as one event— one single, static tone.

Through the example of a physical signal whose grain-rate (i.e. frequency) is manipulated, we can identify the perceptual difference that separates pulsation and tone: the abstraction of time. Pulsations that are perceived as “faster” or “slower” in the temporal domain are transformed into a tones and perceived as “higher or lower” in the pitch domain (or other associations, depending on the culture [1]). It is for this reason that we will, from hereon, consider all time-related events as belonging to the rhythmic domain. For clarity, the term onset and offset is extended to include even the most unclear attacks and decays.

We arrive at the basic disconnect between the two musical domains: the perception of time in pulsation and the perception of tone in frequencies. At slow cycle durations (pulsation), time between onsets is consciously available and onset/offset pairs are distinguishable; at fast cycle durations (frequency) time is not perceptible and individual onset/offset pairs are not accessible. For the rest of the paper, I will discuss time and tone as two distinct musical domains.

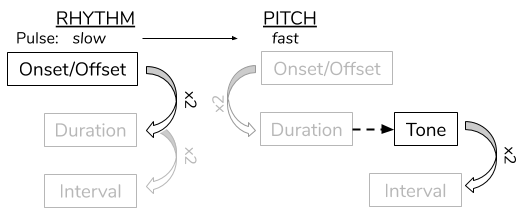
Figure 1

Given this discrepancy, it is important to question why we can continue to search for isomorphisms between these two, non-isomorphic domains (Figure 1). While it is clear that there are vast perceptual differences between the two musical domains, it is interesting to observe that both domains are often approached through proportions (or “intervals,” above). It can be shown that similar cognitive structures serve to compare units within both the temporal and pitch domains.[2] Different musical traditions impose abstract, proportional “maps” onto these domains in the form of tonality, meters, scales, rhythmic patterns, etc. The prevalence of proportional systems across both domains is what encourages us to consider the relationship between these systems.

It is then pertinent to consider the units in either domain which facilitate these proportions, as well as how they can be related. I propose two possibilities for which units may be equated. The first explores durations, fundamental to both pitch and rhythm, as the units of these models. The second, later on in this paper, relates the audible members of each domain (marked in bold in Figure 1).

Basic Proportional Relationships

The harmonic series is a common framework for evaluating integer-based proportional relationships between frequencies. A harmonic series is created by taking a reference frequency (the root) and multiplying it by incrementally-ascending integers. Instead of discussing each harmonic as a fixed frequency, we will use the harmonic series relatively in order to evaluate any  root value. For pulsation and frequency, we take the “unison” and “whole note” as references and multiply them by progressively-ascending integers.

In Figure 2, the bottom row of the left chart represents the root, and the rows above represent integer-multiples of the root. Each row contains three columns containing the pitch, rhythmic, and integer interval with respect to the root. In this first example, we will limit our consideration to a single row of the harmonic series at a time.

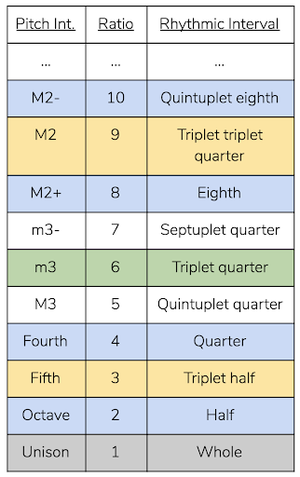
Figure 2

An interesting equivalence suggested by this model is between octaves and double time. Due to the fact that pitch tends to operate below proportions of ≤.5 and rhythm above ≥.5,  it is precisely this 0.5, or 1:2 ratio, in which the two domains share a strong quality. I will consider in greater detail this shared quality later on in the paper.

Considering the connection between tone and time through single harmonic ratios does not prove to be very powerful for a number of reasons. The first disparity is that our “range of hearing” in the temporal domain is comparatively smaller than that of the pitch domain. The human range of beat perception occurs at 0.5-4Hz.[3] As a pulse grows to a length of 2 seconds, events dissociate and a pulse is undetectable. As a root is subdivided beyond than 20 times per second, the pulse converts into pitch. This rhythmic “range of hearing,” from 2 seconds to 1/20 seconds, forms a ratio of 1:40. Pitch, by contrast, can go from 20Hz to 20,000Hz[4]– 25 times larger than rhythm.

Figure 3

The second disparity shown by this model arises when taking a musical perspective. In most musical cultures, scales partition an octave (1:2 ratio) into at least 4 parts. This means that, in the tonal domain, the root (or “tonic”) is able to form very complex ratios with simultaneous or subsequent pitches. Rhythm, however, 1) more commonly features much larger intervallic leaps, and 2) more often features ratios which can be reduced to 1:x (where x is a low integer) and subdivide by x recursively.

It is hypothesized that these rhythmic features are due to our cognitive tendency to relate all temporal events to a perceived beat (called rhythmic “entrainment”)[5] in combination with our preference for events to be grouped recursively in units of 1, 2, and 3 (dubbed “subitization”).[6] Essentially, a beat will be divided into a few small, usually evenly-spaced parts. Those parts are then similarly divided again. This process repeats until we see strong preferences for the ratios highlighted in Figure 2. In the figure, blue columns are products of 2-subdivisions (tuplets), yellow columns are products of 3-subdivisions (triplets), and green are products off 2- and 3-subdivisions. Pitch, however, does not exhibit these same tendencies.

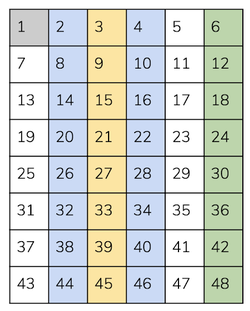
Figure 4

x : (x+1)

Above, I considered one row of the harmonic series at a time. In this example, I look at two adjacent rows occurring simultaneously (cross-rhythms and dyads). Two adjacent rows form phasing ratios, meaning that the two pulse/frequency streams form a ratio of x:(x+1). While these ratios offer a very limited window to the harmonic series, they present characteristics useful for drawing isomorphisms.

Considering phasing relationships within pulsation and frequency has several advantages. First, two cycles going in and out of phase alignment in a periodic fashion results in a perceivable, higher-level structure. This higher-level structure is perceivable ubiquitously across both temporal and pitch domains. In time, the higher level is felt as a longer temporal cycle. The leftmost depiction in Figure 5 demonstrates how- at slower pulsations- a higher level arises from the oscillation between maximal alignment and misalignment of the grains. In tone, the higher level is perceived as a periodic amplitude modulation, called “beating.”[7] The rightmost depiction demonstrates how the amplitude envelopes of each grain combine, forming a “hairpin” shape in the amplitude. This higher level can even be perceived as a separate pitch if the cycling frequency is sufficiently high.[8] Simply put, everytime two phasing pulsations or frequencies are played, we identify the root (the “1”) such that the initial x:(x+1) becomes x:(x+1):1.

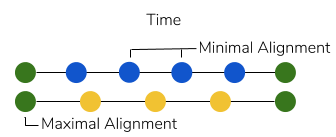
Figure 5a

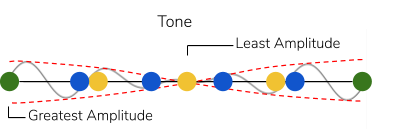
Figure 5b

The next advantage of this approach is the ability for pulsations in the temporal domain to employ ratios beyond 1:x. With the opportunity for simultaneity, we are able to identify common ratios between the pitch and rhythm domains such as 2:3 and 3:4. These polyrhythms are extremely common across a vast part of the musical geography.[9] The pitch equivalents of these ratios depict themselves through the just-4th and just-5th dyads– also extremely common intervals. Perceptually-speaking, all phasing polyrhythms x:(x+1) in music generally have the same perceived “beating” quality, meaning that 6:7, for example, resembles 17:18 simply because they both phase.[10] Theoretically, there exists isomorphisms between any two phasing polyrhythms and dyads. From a performance perspective however, the fact that musicians experience much greater difficulty when attempting higher-integer phasing ratios in polyrhythms than in dyads argues against this general comparison.[11]

x : (x+n)

It is interesting to note that, performance-wise, the ratio 2:x- which manifests itself in many examples within the pitch domain- is very easy to produce rhythmically. In an attempt to explore more complex intervals, such as 2:x, within the temporal domain, I consider what happens to x:(x+n) when n>1. In other words, considering non-adjacent rows of the harmonic series.

Above, we saw that n=1yields a simple cycle away from and back to alignment. For n>1 however, x and (x+n) must go through several rounds of phasing before re-aligning. Put simply, while approaching alignment, both streams cross each other at an imperfect alignment and go through additional round(s) of phasing before aligning. These extra phases occur n times. This process is visible in Figure 6– faux-alignments are depicted with dotted boxes. Clockwise, the three boxes depict a global alignment, followed by a local maximum where the 31-stream is lagging, and finally a local maximum where the 28-stream is lagging. As the values x and (x+n) increase, faux-alignments become more aligned and, at high enough values, become indiscernible from total alignment. This actually results in a perceived beating frequency of n, regardless of whether n is the common factor of both streams. Ultimately, the frequency of a beat between any two rows in the harmonic series is their difference, n.

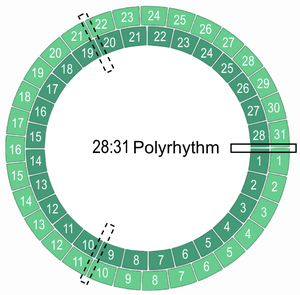
Figure 6

This phenomenon is perceivable in both low and high x-values (pulsations and frequencies). Though, mentioned above, faux-alignments are less convincing beat-replacements in low x-values (pulsations). Figure 6 is an example of a phasing pulsation with a beating pattern that, at a specific tempi, can either be perceived as one long beat or three faster beats. As mentioned however, from a musical perspective, the relative difficulty of producing such complex polyrhythms and their rarity compared to tone production argues against this comparison.

A disparity highlighted by this model appears in the temporal domain, where one pulsation is cognitively elected as the tactus- or reference pulse- in polyrhythms.[12] When one pulse is being entrained, any other pulse is heard relative- and subordinate-to the initial pulse. This is most likely due to our limited capacity of entraining to one single pulse at a time.[13] Pitch perception, unlike rhythm, does not elect a fixed reference pitch out of a dyad (in non-tonal hierarchical contexts) and has only a slight preference for the faster frequency.[14]

Finally, we can consider including more than two adjacent proportions. While it is common for frequencies to form ratios with three or more values which do not share common factors (e.g. dominant: 4:5:(6):7), it is virtually impossible to find a polyrhythmic equivalent in music or psychology literature. Similarly to our previous discussion on the “range of hearing,” here, pitch ultimately has a much higher tolerance for stacking non-inclusive proportions than rhythm.

To conclude, thinking of pitch and time in terms of their shared acoustical properties (pulses and frequencies) opens up many interesting avenues for inter-domain connections to be made. Contributions like double time and octave equivalence, beating, and the different proportional “domains” that pitch and rhythm commonly exemplify all offer valuable insight into further isomorphic models. Admittedly, an approach which focuses solely on proportional relationships between pitch and rhythm ultimately struggles to connect with music.

Divisive Cyclic Models

A powerful route opens up when considering an abstraction of time in the pitch domain. We know that frequencies in octave relations are perceived with very high similarities.[15] That is, a frequency value x and its octave transpositions are nearly interchangeable. This phenomenon is called “pitch class.” Unlike frequencies, which map linearly, pitch classes can be mapped on a circle. To do this, we draw a line from any frequency x to it’s octave 2x and wrap the ends together, forming a circle. The frequencies on the line between x and 2x retain their relative distances as they bend around. Suddenly, we have a circle depicting not the frequency values of points, but proportions/intervals between them. The opposite ends of the circle, which represent the greatest intervallic distance, are separated by a 1:2 interval (a tritone). This cycle can be demarcated by any number of pitch-classes in any interval pattern.

This carries the paper to the second model of pitch/time isomorphisms: cyclic models. We can draw an isomorphism between the cyclic models of pitch-class and rhythm. In the temporal domain, a cyclic model arises when a pulsation is wrapped onto itself so that a single onset serves as both the beginning and end of a fixed duration cycle. Mentioned earlier, this model draws an isomorphism between the two audible units of each domain: tones (in the form of pitch classes) and onsets. Pitch-classes demarcate points on the pitch-class circle, while onsets demarcate points on the rhythm circle. Isomorphisms can only be drawn from “strong isomorphic” circles; circles with the same number and spacing-pattern of divisions.

There are two hurdles to overcome in drawing this isomorphism. First is the issue of equating onset/offset and tones. Second is the initial disparity between time and tone. The disjunction between onset/offset and pitch is depicted in Figure 1. The audible members of each domain- tones and onset- exist at different levels of abstraction. While evenly-cycling onsets create a repeating duration, pitches (which are two repeating durations), however, give a proportion; a “tonal interval.” This means that intervals within the temporal cycle will not have the same values as intervals along the pitch cycle.

The difference manifests itself when considering the extremities of either circle. For the rhythm circle, the opposite ends will feature a ratio of 1:2; pitch, 1:2. In drawing this isomorphism, however, we can overlook this discrepancy. We are not attempting to equate the units of the circle. Instead, we are interested in the patterns of distances formed by points along both circle depictions.

The next hurdle, pointed out at the beginning of the paper, is mitigating time across the two models. In a rhythm circle, time always moves in one direction. In a pitch-class circle, time does not exist. This can be easily overcome using the simple depiction in Figure 7.

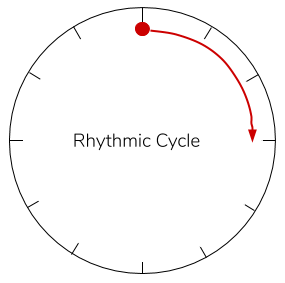
Figure 6a

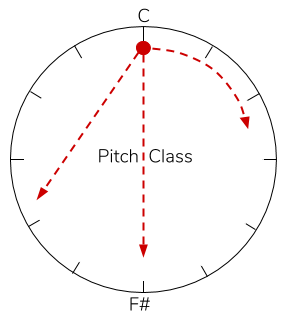
Figure 6b

Consider a ball which can travel along a circumference of the pitch-class or rhythm circle. A point sounds whenever the ball moves onto it. In a pitch class circle, the ball can be stagnant, slide, or skip instantaneously in any direction (higher, lower) across the real pitches. However, in a rhythm circle, the ball must continuously move in the same direction (forward) and pass between every point along the circle.

This connection ends up being quite powerful. The most notable isomorphisms comes from parallel intervallic patterns between temporal and pitch-class cycles. In his paper, “Cognitive Isomorphisms between Pitch and Rhythm in World Musics,” Pressing points out 24 pages worth of isomorphisms between common two 12-cycles: 12-tET in Western music and Sub-Saharan African 12-beat-cycle music. Beyond his discoveries, isomorphisms between expressive musical behaviors are also revealed by mapping them into these cycles. Pitch slides and inflections find their counterparts in rubato and tempo stretching. Detunings have their counterpart with rhythmic swinging. The direction of swing (relative to the beat) is isomorphic with the with sharp vs. flat detuning (relative to the scale).

The main disparity exemplified by this model is similar to the previous model. Musical rhythm commonly occurs as recursive divisions of the circle through small integer values. Pitch, as in many cultures, does not subdivide the circle recursively or as finely. This difference likely arises due to rhythm’s tendency for recursive subdivision, where it is hypothesized that tonal scales (pitch-class sets) arise from a stacked interval.[16]

Ultimately, musical systems which employ equal divisions of a timespan (for rhythm) and an octave (for pitch) are prevalent in a vast number of musical cultures. This model is supported by a broad terrain for making connections from one tradition to another. Cyclic conceptions of music, being so prevalent, provide further platforms for exploration. Perhaps these models could take on a more literal form; a “rhythm-class” cycle or a linear pitch cycle rooted in hertz values.

Conclusion

While I have only investigated a few models, there are many more paths to explore. We can venture down additive cyclic models, pitch vs. temporal hierarchies, isomorphic serial transformations, temporal equivalent for non-octaviating scales, tonal equivalent for rhythmic integration, etc. Several benefits arise from the pursuit of this topic. Having a greater understanding of these two musical domains could likewise advance the understanding of musics across cultures by proposing new venues for analysis.  Established isomorphic models could suggest new venues for analysis within the two domains themselves, opening up new terrains for both theorists, composers, and musicologists alike. Both connections and disparities that arise between the temporal and tonal domains work hand-in-hand with the cognitive processes guiding a listener. Addressing these models can clarify the nuances of music perception and cognition across the two domains.

Note

As a student, I note that my understanding of this subject is still nascent and developing. My only goal in this article is to provide a comprehensive summary for new artists and analysts; for those looking to tackle contemporary theoretical issues and bring together knowledge from different fields in music. I wrote this because the idea of similar musical structures in time and tone pushed me to advance my knowledge in several fields: ethnomusicology, music theory, auditory perception and cognition, and acoustics. It pushed me to confront the limits of my understanding of important musical concepts, and- ultimately- develop better control of them. My hope is that this article can deliver these nuances to the reader.

- Julien Pallière, 2019

Notes

[1] Ashley, Richard. “Musical Pitch Space Across Modalities- Spatial and Other Mappings Through Language and Culture.” pp. 64–71.

[2] Krumhansl, Carol L. “Rhythm and Pitch in Music Cognition.” Psychological Bulletin, vol. 126, no. 1, 2000, pp. 159–179.

[3] London, Justin. “Hearing in Time.” 2004.

[4] Longstaff, Alan, and Alan Longstaff. “Acoustics and Audition.” Neuroscience, BIOS Scientific Publishers, 2000, pp. 171–184.

[5] Nozaradan, S., et al. “Tagging the Neuronal Entrainment to Beat and Meter.” Journal of Neuroscience, vol. 31, no. 28, 2011, pp. 10234–10240.

[6] Repp, Bruno H. “Perceiving the Numerosity of Rapidly Occurring Auditory Events in Metrical and Nonmetrical Contexts.” Perception & Psychophysics, vol. 69, no. 4, 2007, pp. 529–543.

[7] Vassilakis, Panteleimon Nestor. “Perceptual and Physical Properties of Amplitude Fluctuation and Their Musical Significance.” 2001.

[8] Smoorenburg, Guido F. “Audibility Region of Combination Tones.” The Journal of the Acoustical Society of America, vol. 52, no. 2B, 1972, pp. 603–614.

[9] Pressing, Jeff, et al. “Cognitive Multiplicity in Polyrhythmic Pattern Performance.” Journal of Experimental Psychology: Human Perception and Performance, vol. 22, no. 5, 1996, pp. 1127–1148.

[10] Pitt, Mark A., and Caroline B. Monahan. “The Perceived Similarity of Auditory Polyrhythms.” Perception & Psychophysics, vol. 41, no. 6, 1987, pp. 534–546.

[11] Peper, C. E., et al. “Frequency-Induced Phase Transitions in Bimanual Tapping.” Biological Cybernetics, vol. 73, no. 4, 1995, pp. 301–309.

[12] Handel, Stephen, and James S. Oshinsky. “The Meter of Syncopated Auditory Polyrhythms.” Perception & Psychophysics, vol. 30, no. 1, 1981, pp. 1–9.

[13] Jones, Mari R., and Marilyn Boltz. “Dynamic Attending and Responses to Time.” Psychological Review, vol. 96, no. 3, 1989, pp. 459–491.

[14] Palmer, Caroline, and Susan Holleran. “Harmonic, Melodic, and Frequency Height Influences in the Perception of Multivoiced Music.” Perception & Psychophysics, vol. 56, no. 3, 1994, pp. 301–312.

[15] Deutsch, Diana, and Edward M. Burns. “Intervals, Scales, and Tuning.” The Psychology of Music, Academic Press, 1999, pp. 252–256.

[16] “Errata: Aspects of Well-Formed Scales.” Music Theory Spectrum, vol. 12, no. 1, 1990, pp. 171–171.

Additional References

Pressings, J. “Cognitive Isomorphisms between Pitch and Rhythm in World Musics: West Africa, The Balkans and Western Tonality.” 1975, Pp 38-61.

London, J. “Some Non-Isomorphisms Between Pitch And Time.” Journal of Music Theory, vol. 46, no. 1-2, Jan. 2002, pp. 127–151.

Rahn, John. “On Pitch or Rhythm: Interpretations of Orderings of and in Pitch and Time.” Perspectives of New Music, vol. 13, no. 2, 1975, p. 182.

Stevens, Catherine. “Cross-Cultural Studies of Musical Pitch and Time.” Acoustical Science and Technology, vol. 25, no. 6, 2004, pp. 433–438.

Bar-Yosef, Amatzia. “A Cross-Cultural Structural Analogy Between Pitch And Time Organizations.” Music Perception: An Interdisciplinary Journal, vol. 24, no. 3, 2007, pp. 265–280.

Stockhausen, Karlheinz. “Structure and Experimential Time.” Die Reihe, vol. 2, 1958, p. 64.

Stockhausen, Karlheinz, and Elaine Barkin. “The Concept of Unity in Electronic Music.” Perspectives of New Music, vol. 1, no. 1, 1962, p. 39.

Grisey, Gérard. “Tempus Ex Machina:A Composers Reflections on Musical Time.” Contemporary Music Review, vol. 2, no. 1, 1987, pp. 239–275.

Roads, Curtis. Microsound. MIT, 2004.

Zanto, Theodore P., et al. “Neural Correlates of Rhythmic Expectancy.” Advances in Cognitive Psychology, vol. 2, no. 2, Jan. 2006, pp. 221–231.

Grahn, Jessica A. “Neural Mechanisms of Rhythm Perception: Current Findings and Future Perspectives.” Topics in Cognitive Science, vol. 4, no. 4, 2012, pp. 585–606.